动态规划
动态规划
一、基础知识
1.1 定义:
动态规划(Dynamic Programming,DP)是运筹学的一个分支,是求解决策过程最优化的过程。20世纪50年代初,美国数学家贝尔曼(R.Bellman)等人在研究多阶段决策过程的优化问题时,提出了著名的最优化原理,从而创立了动态规划。动态规划的应用极其广泛,包括工程技术、经济、工业生产、军事以及自动化控制等领域,并在背包问题、生产经营问题、资金管理问题、资源分配问题,最短路径问题和复杂系统可靠性问靠性问题等中取得了显著的效果。
动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中,可能会有许多可行解。每一个解都对应于一个值,我们希望找到具有最优值的解。动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。若用分治法来解这类问题,则分解得到的子问题数目太多,有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。这就是动态规划法的基本思路。具体的动态规划算法多种多样,但它们具有相同的填表格式。
1.2 总结
动态规划的所有问题,都是按照下面的思维模式进行解决的。
题目只要问最值,但是不在乎得到最值的解法,基本可以考虑使用动态规划解决问题
【状态】:问题求什么,要什么,我们dp的因变量就是什么,自变量根据题目要求,为物品和容量
【状态方程】:确定好了状态,就要看看这个父问题如何转换为子问题了,这也是状态方程要解决的
【初始化】:主要是看有没有要求得到最值的时候,满负载
【状态的计算过程】:怎么算出状态的答案
【考虑压缩空间】:自变量如果能从物品和容量单纯的变成容量,那自然是好事
二、背包问题
背包问题(Knapsack problem)是一种组合优化的NP(Non-deterministic PolynomialNP问题是指可以在多项式的时间里验证一个解的问题。NP问题的另一个定义是,可以在多项式的时间里猜出一个解的问题。)完全问题。问题可以描述为:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。相似问题经常出现在商业、组合数学,计算复杂性理论、密码学和应用数学等领域中。也可以将背包问题描述为决定性问题,即在总重量不超过W的前提下,总价值是否能达到V?它是在1978年由Merkle和Hellman提出的。
1.1 背包问题
1.1.1 问题描述
有n个物品,它们有各自的体积和价值,现有给定容量的背包,如何让背包里装入的物品具有最大的价值总和?
为方便讲解和理解,下面讲述的例子均先用具体的数字代入,即:eg:number=4,capacity=8
| i(物品编号) | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| w(体积) | 2 | 3 | 4 | 5 |
| v(价值) | 3 | 4 | 5 | 6 |
1.1.2 总体思路
根据动态规划解题步骤(问题抽象化、建立模型、寻找约束条件、判断是否满足最优性原理、找大问题与小问题的递推关系式、填表、寻找解组成)找出01背包问题的最优解以及解组成,然后编写代码实现。
1.1.3 动态规划的原理
动态规划与分治法类似,都是把大问题拆分成小问题,通过寻找大问题与小问题的递推关系,解决一个个小问题,最终达到解决原问题的效果。但不同的是,分治法在子问题和子子问题等上被重复计算了很多次,而动态规划则具有记忆性,通过填写表把所有已经解决的子问题答案纪录下来,在新问题里需要用到的子问题可以直接提取,避免了重复计算,从而节约了时间,所以在问题满足最优性原理之后,用动态规划解决问题的核心就在于填表,表填写完毕,最优解也就找到。
最优性原理是动态规划的基础,最优性原理是指“多阶段决策过程的最优决策序列具有这样的性质:不论初始状态和初始决策如何,对于前面决策所造成的某一状态而言,其后各阶段的决策序列必须构成最优策略”。
1.1.4 背包问题的解决过程
在解决问题之前,为描述方便,首先定义一些变量:Vi表示第 i 个物品的价值,Wi表示第 i 个物品的体积,定义V(i,j):当前背包容量 j,前 i 个物品最佳组合对应的价值,同时背包问题抽象化(X1,X2,…,Xn,其中 Xi 取0或1,表示第 i 个物品选或不选)。
1、建立模型,即求max(V1X1+V2X2+…+VnXn);
2、寻找约束条件,W1X1+W2X2+…+WnXn<capacity;
3、寻找递推关系式,面对当前商品有两种可能性:
- 包的容量比该商品体积小,装不下,此时的价值与前i-1个的价值是一样的,即V(i,j)=V(i-1,j);
- 还有足够的容量可以装该商品,但装了也不一定达到当前最优价值,所以在装与不装之间选择最优的一个,即V(i,j)=max{V(i-1,j),V(i-1,j-w(i))+v(i)}。
其中V(i-1,j)表示不装,V(i-1,j-w(i))+v(i) 表示装了第i个商品,背包容量减少w(i),但价值增加了v(i);
由此可以得出递推关系式:
- j<w(i) V(i,j)=V(i-1,j)
- j>=w(i) V(i,j)=max{V(i-1,j),V(i-1,j-w(i))+v(i)}
这里需要解释一下,为什么能装的情况下,需要这样求解(这才是本问题的关键所在!):
可以这么理解,如果要到达V(i,j)这一个状态有几种方式?
肯定是两种,第一种是第i件商品没有装进去,第二种是第i件商品装进去了。没有装进去很好理解,就是V(i-1,j);装进去了怎么理解呢?如果装进去第i件商品,那么装入之前是什么状态,肯定是V(i-1,j-w(i))。由于最优性原理(上文讲到),V(i-1,j-w(i))就是前面决策造成的一种状态,后面的决策就要构成最优策略。两种情况进行比较,得出最优。
4、填表,首先初始化边界条件,V(0,j)=V(i,0)=0;
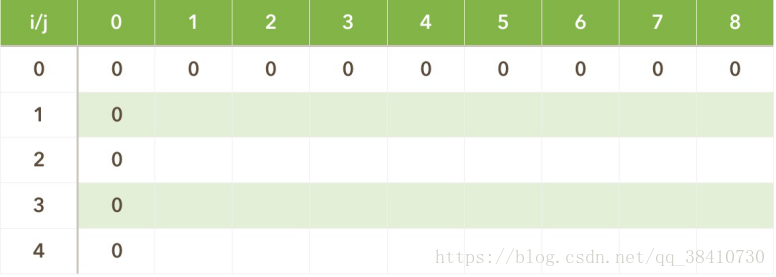
然后一行一行的填表:
- 如,i=1,j=1,w(1)=2,v(1)=3,有j<w(1),故V(1,1)=V(1-1,1)=0;
- 又如i=1,j=2,w(1)=2,v(1)=3,有j=w(1),故V(1,2)=max{ V(1-1,2),V(1-1,2-w(1))+v(1) }=max{0,0+3}=3;
- 如此下去,填到最后一个,i=4,j=8,w(4)=5,v(4)=6,有j>w(4),故V(4,8)=max{ V(4-1,8),V(4-1,8-w(4))+v(4) }=max{9,4+6}=10……
所以填完表如下图:
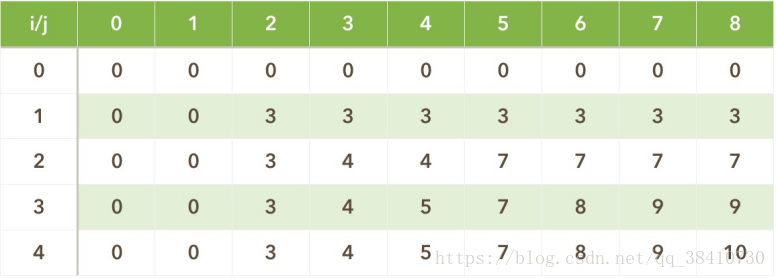
5、表格填完,最优解即是V(number,capacity)=V(4,8)=10。
1.1.5 代码实现
public static void main(String[] args) {
// n 表示装入苹果的个数, v表示背包的容量
int n=4, v=8;
// 体积
int [] volume = new int[]{0, 2, 3, 4, 5 };
// 价值
int [] value = new int[]{0, 3, 4, 5, 6 };
int [][] dp = new int[10][10];
for (int i=1;i<=n;i++){
for (int j=1; j<=v; j++){
if (j < volume[i]){
dp[i][j] = dp[i-1][j];
}else {
dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j- volume[i]]+value[i]);
}
}
}
for (int i=0; i<5; i++){
for (int j=0; j<9; j++){
System.out.print(dp[i][j]+" ");
}
System.out.println();
}
System.out.println(dp[n][v]);
}